Назва проекту
Теорема, що не втратила актуальність
на протязі тисячоліть
Автори проекту
Учні групи "Науковці"
Тема дослідження
Теорема Піфагора та способи її доведення
Проблема дослідження
Теорема Піфагора та способи її доведення
Гіпотеза дослідження
Крім авторського доведення існують і інші варіанти,
які потребують уваги
Мета дослідження
Розглянути формулювання теореми Піфагора та
дослідити способи її доведення
Хід і результати дослідження
Теоре́ма Піфаго́ра — одна із основоположних теорем евклідової геометрії, котра встановлює співвідношення між сторонамипрямокутного трикутника. Вважається, що вона доведена грецьким математиком Піфагором, на честь котрого вона названа (є й інші версії, зокрема альтернативна думка, що ця теорема у загальному вигляді була сформульована математиком-піфагорійцем Гіппасом).
Теорема
Теорема звучить так:
 |
| Теорема Піфагора: a2 + b2 = c2 |
У прямокутному трикутнику площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів, побудованих на катетах.
Позначивши довжину гіпотенузи трикутника як c, а довжини катетів як a та b, отримаємо такі формули:
Таким чином, теорема Піфагора встановлює співвідношення, яке дозволяє визначити сторону прямокутного трикутника, знаючи довжини двох інших. Відповідно, в алгебраїчній інтерпретації теорему можна сформулювати так:
У прямокутному трикутнику сума квадратів катетів дорівнює квадрату гіпотенузи.
Теорема Піфагора є окремим випадком теореми косинусів, котра визначає співвідношення між сторонами довільного трикутника.
Також доведено зворотне твердження (називають також зворотною до теореми Піфагора):
Для будь-яких трьох додатних чисел a, b і c, для яких виконується рівняння
a² + b² = c²,
існує прямокутний трикутник з катетами a та b і гіпотенузою c.
Історія
Історію теореми можна розділити на чотири частини: знання про Піфагорові числа, знання про відношення сторін в прямокутному трикутнику, знання про відношення суміжних кутів та доведення теореми.
Мегалітичні споруди близько 2500 до н. е. в Єгипті та Північній Європі містять прямокутні трикутники із сторонами з цілих чисел. Бартель ван дер Варден висловив гіпотезу, що в ті часи Піфагорові числа були знайдені алгебраїчно.
Написаний між 2000 та 1876 до н. е. папірус часів Середнього Єгипетського царства Berlin 6619 містить задачу, розв'язком якої є числа Піфагора.
Написана під час правління Хамурапі Великого (між 1790 і 1750 до н.е) вавилонська табличка Plimpton 322 містить багато записів, тісно пов'язаних із числами Піфагора.
В сутрах Будхаяни, які датуються за різними версіями 8-им чи 2-им століттям до н. е. в Індії, містить Піфагорові числа виведені алгебраїчно, формулювання теореми Піфагора та геометричне доведення для рівнобедренного прямокутного трикутника.
В сутрах Апастамби (близько 600 до н. е.) міститься числове доведення теореми Піфагора з використанням обчислення площі. Ван дер Варден вважає, що воно було засноване на традиціях попередників. Згідно з Альбертом Бурком, це оригінальне доведення теореми і він припускає, що Піфагор відвідав Араконам і скопіював його.
Піфагор, роки життя якого зазвичай приймають за 569 — 475 до н. е. використовує алгебраїчні методи розрахунку піфагорових трійок, згідно з Прокловими коментарями до Евкліда. Прокл, однак, жив між 410 і 485 роками н. е. Згідно з Томасом Гізом, немає ніяких вказівок на авторство теореми протягом п'яти століть після Піфагора. Однак такі автори як Плутарх або Ціцерон приписали теорему Піфагору у такий спосіб, ніби авторство було широко відоме і безсумнівне.
Близько 400 до н. е. згідно з Проклом, Платон дав метод розрахунку піфагорових трійок, що поєднував алгебру та геометрію. Близько 300 до н. е., в Началах Евкліда маємо найдавніше аксіоматичне доведення, яке збереглося до наших днів.
Написана десь між 500 до н. е. і 200 до н. е., китайська математична книга «Чу Пей» (周髀算经) дає візуальне доведення теореми Піфагора, яка в Китаї називається теорема Гугу (勾股定理), для трикутника із сторонами (3, 4, 5). Під час правління династії Хань, з 202 до н. е. до 220 н. е. Піфагорові трійки з'являються в книзі «Дев’ять розділів математичного мистецтва» разом із згадкою про прямокутні трикутники.
Вперше зафіксовано використання теореми в Китаї, де вона відома як теорема Гугу (勾股定理) та в Індії, де вона відома як теорема Баскара.
Багато дискутується, чи була теорема Піфагора відкрита один раз чи багато разів. Бойер (1991) вважає, що знання, виявлені в Шульба Сутрах, можуть бути месопотамського походження.
Доведення
Алгебраїчне доведення
Відомо понад сто доведень теореми Піфагора. Тут представлено доведення, засноване на теоремі існування площі фігури:
- Розташуємо чотири однакові прямокутні трикутники так, як це зображено на малюнку.
- Чотирикутник зі сторонами c є квадратом, оскільки сума двох гострих кутів
 , а розгорнутий кут —
, а розгорнутий кут — 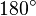 .
. - Площа всієї фігури рівна, з одної сторони, площі квадрата зі стороною «a+b», а з іншої — сумі площ чотирьох трикутників і внутрішнього квадрата.
Що і необхідно було довести.
За подібністю трикутників
Нехай ABC — прямокутний трикутник, в якому кут C прямий, як показано на малюнку. Проведемо висоту з точки C, і назвемо Hточку перетину з стороною AB. Утворений трикутник ACH подібний до трикутника ABC, оскільки вони обидва прямокутні (за визначенням висоти), і в них спільний кут A, очевидно третій кут буде в цих трикутників також однаковий. Аналогічно міркуючи, трикутник CBH також подібний до трикутника ABC. З подібності трикутників: Якщо
тоді
Це можна записати у вигляді
Якщо додати ці дві рівності, отримаєм
Іншими словами, Теорема Піфагора:
Доведення Евкліда
В Евклідових «Началах», теорема Піфагора доведена методом паралелограмів. Нехай A, B, C — вершини прямокутного трикутника, з прямим кутом A. Опустимо перпендикуляр з точки A на сторону, протилежну до гіпотенузи в квадраті, побудованому на ній. Лінія ділить квадрат на два прямокутники, кожен з яких має таку саму площу, що й квадрати, побудовані на катетах. Головна ідея при доведенні полягає в тому, що верхні квадрати перетворюються на паралелограми такої самої площі, а тоді повертаються і перетворюються на прямокутники в нижньому квадраті і знову при незмінній площі.
Для формального доведення, нам необхідні чотири елементарні леми:
- Якщо дві сторони одного трикутника і кут між ними дорівнюють відповідно двом сторонам та куту між ним іншого трикутника, то такі трикутники рівні (сторона-кут-сторона).
- Площа трикутника дорівнює половині площі паралелограма, що має таку саму основу і таку саму висоту.
- Площа прямокутника дорівнює добутку двох суміжних сторін.
- Площа квадрата дорівнює добутку двох його сторін (випливає з третьої леми).
Тоді кожен верхній квадрат пов'язаний з трикутником, конгруентним з іншим трикутником, який пов'язаний поворотом з одним із двох прямокутників, що утворюють нижній квадрат.
Перейдемо до доведення:
- Нехай ACB — прямокутний трикутник з прямим кутом CAB.
- На кожній стороні BC, AB, і CA побудуємо квадрати CBDE, BAGF та ACIH в такому ж порядку. Побудова квадратів тут же вимагає попередньої теореми Евкліда, і залежить від постулату паралельності.[7]
- З точки A проводимо пряму паралельну до BD і CE. Вона перпендикулярно перетне відрізки BC та DE в точках K та L, відповідно.
- Проведемо відрізки CF і AD, отримаємо трикутники BCF і BDA.
- Кути CAB і BAG — прямі; відповідно точки C, A і G — колінеарні. Так само B, A і H.
- Кути CBD і FBA — обидва прямі; тоді кут ABD дорівнює куту FBC, оскільки обидва є сумою прямого кута та кута ABC.
- Трикутники ABD та FBC рівні за двома сторонами та кутом між ними.
- Оскільки точки A, K і L — колінеарні, площа прямокутника BDLK дорівнює двом площам трикутника ABD (BDLK = BAGF = AB2)
- Аналогічно міркуючи, отримаємо CKLE = ACIH = AC2
- З одного боку площа CBDE дорівнює сумі площ прямокутників BDLK та CKLE, а з другого боку площа квадрата BC2, або AB2 + AC2 = BC2.
"Піфагорові штани" — жартівлива назва цього доказу.
Використовуючи диференціали
До теореми Піфагора можна прийти розглядом залежності величини гіпотенузи від приросту сторони (див. малюнок праворуч), застосувавши невелике обчислення.
В результаті приросту сторони a, з подібних трикутників для нескінченно малих приростів:
Застосуємо розділення змінних.
Інтегруючи, отримаємо:
Якщо a = 0 тоді c = b, отже «константа» — b2. Тоді
Як можна побачити, квадрати отримано завдяки пропорції між приростами та сторонами, тоді як сума є результатом незалежного внеску приростів сторін, що не очевидно з геометричних доведень. В цих рівняннях da і dc — відповідно нескінченно малі прирости сторін a і c. Але замість них ми використовуємо Δa і Δc, тоді границя їхнього відношення, якщо вони прямують до нуля, дорівнює da/dc (похідній) і також дорівнює c/a (відношенню довжин сторін трикутників), в результаті чого отримуємо диференціальне рівняння.
Доведення Мьольманна
Площа даного трикутника з однієї сторони дорівнює 1/2ab, а з другої - 1/2pr, де р - півпериметр, r- радіус вписаного кола. В прямокутному трикутнику r=1/2(a+b-c).
Маємо 0,5ab=0,5pr=0,5(a+b+c)·0,5(a+b-c)
0,5ab=0,5(a+b+c)·0,5(a+b-c)
аb=0,5(a2 + ab – ac + ab + b2 – bc + ca + cb - c2)
аb=0,5(a2 +b2- c2 +2ab)/·2
2аb=a2 +b2- c2 +2ab
a2 + b2- c2 =0
Розташуємо чотири однакові прямокутні трикутники так, як це зображено на малюнку.
Чотирикутник зі сторонами c є квадратом, оскільки сума двох гострих кутів  , а розгорнутий кут —
, а розгорнутий кут — 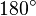 .
.
 , а розгорнутий кут —
, а розгорнутий кут — 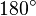 .
.
Площа всієї фігури рівна, з одної сторони, площі квадрата зі стороною «a+b», а з іншої — сумі площ чотирьох трикутників і внутрішнього квадрата.
Що і необхідно було довести.
Адитивний метод (метод розкладу)
Існує цілий ряд доведень теореми Піфагора, в яких квадрати, побудовані на катетах і на гіпотенузі, розрізають так, що кожної частини квадрата, побудованого на гіпотенузі, відповідає частина одного з квадратів, побудованих на катетах. У всіх цих випадках для розуміння докази достатньо одного погляду на креслення; міркування тут може бути обмежене єдиним словом: "Дивись!", Як це робилося в творах стародавніх індуських математиків. Слід, однак, зауважити, що насправді доказ можна вважати повним, поки ми не довели рівності всіх відповідних один одному частин. Це майже завжди досить важко зробити, однак може (особливо при великій кількості частин) зажадати досить тривалої роботи.
Доведення Епштейна
Тут в якості складових частин розкладання фігурують виключно трикутники. Щоб розібратися в кресленні, зауважимо, що пряма CD проведена перпендикулярно прямий EF.
Розкладання на трикутники можна зробити і більш наочним, ніж на малюнку.
Розкладання на трикутники можна зробити і більш наочним, ніж на малюнку.
Доведення Нільсена
На малюнку допоміжні лінії змінені за пропозицією Нільсена.
Доведення Бетхера
На малюнку дано досить наочне розкладання Бетхер.
Доведення Перігаля
У підручниках нерідко зустрічається розкладання зазначене на малюнку (так зване "колесо з лопатями"; це доказ знайшов Перігаль). Через центр O квадрата, побудованого на більшій катета, проводимо прямі, паралельну і перпендикулярну гіпотенузі. Відповідність частин фігури добре видно з креслення
Доведення Гутхейля
 Зображене на малюнку розкладання належить Гутхейль; для нього характерне наочне розташування окремих частин, що дозволяє відразу побачити, які спрощення спричинить за собою випадок рівнобедреного прямокутного трикутника.
Зображене на малюнку розкладання належить Гутхейль; для нього характерне наочне розташування окремих частин, що дозволяє відразу побачити, які спрощення спричинить за собою випадок рівнобедреного прямокутного трикутника.Ще декілька доведень
Висновки
Отже, провівши наше дослідження, ми дізналися формулювання теореми Піфагора та встановили, що вона має велику кількість різноманітних варіантів доведень.
Корисні ресурси
http://uk.wikipedia.org/wiki/Теорема_Піфагора
http://svitppt.com.ua/geometriya/sposobi-dovedennya-teoremi-pifagora.html
http://kucherenkolyada.blogspot.com/p/blog-page_25.html
http://www-formula.ru/index.php/2011-09-22-02-35-26
http://zno.academia.in.ua/mod/book/view.php?id=3016&chapterid=685
https://matematikamoysu.wordpress.com/відеотека/
http://svitppt.com.ua/geometriya/sposobi-dovedennya-teoremi-pifagora.html
http://kucherenkolyada.blogspot.com/p/blog-page_25.html
http://www-formula.ru/index.php/2011-09-22-02-35-26
http://zno.academia.in.ua/mod/book/view.php?id=3016&chapterid=685
https://matematikamoysu.wordpress.com/відеотека/




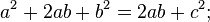


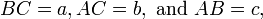







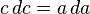








Немає коментарів:
Дописати коментар